CONTOH SOAL DAN PEMBAHASAN

1. Sebuah peluru ditembakkan condong ke atas dengan kecepatan awal 1,4 x 10³ m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2 x 10^5 m. Bila g = 9,8 m/s², maka hitunglah besar sudut elevasinya!
Pembahasan:
Diketahui:
vo = 1,4 x 10³ m/s
xterjauh = 2 x 10^5 m
g = 9,8 m/s²
Ditanya: sudut elevasi (α)
Jawab:

2. Peluru A dan B ditembakkan dari senapan yang sama dengan sudut elevasi berbeda. Peluru A dengan sudut 30˚ dan peluru B dengan sudut 45˚. Tentukan perbandingan tinggi maksimum yang dicapai peluru A dan B!

Pembahasan:

Diketahui:

 αA = 30°

 αB = 45°

Ditanya: perbandingan tinggi maksimum peluru A dan B

Jawab:

Sehingga perbandingan tinggi maksimum peluru A dan B adalah 1:2

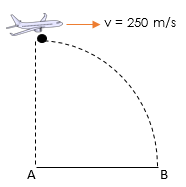
3. Sebuah pesawat terbang bergerak mendatar dengan kecepatan 250 m/s melepaskan bom dari ketinggian 2000 m. Jika bom jatuh di B dan g = 10 m/s², maka hitunglah jarak AB!

Pembahasan:

Diketahui:

vx = 250 m/s

h atau y = -2000 m (negatif (-) karna arah bomnya kebawah)

g = 10 m/s²

Ditanya: jarak AB (xAB)

Jawab:

Tinjau gerakan pada sumbu x (mendatar), yaitu gerak lurus beraturan (GLB) dengan kecepatan vx, sehingga koordinat x dicari dengan rumus:

x = vx.t

x = 250.t

Jadi untuk menghitung x kita harus mencari terlebih dahulu nilai t (waktu yang dibutuhkan bom tersebut untuk sampai di B). Dengan meninjau pada sumbu y (GLBB), didapatkan:

 Gerakan bom merupakan gerakan jatuh bebas, sehingga v0y = 0. Maka:

Sehingga jarak AB:

x = 250.t

x = 250(20) = 5000 m

(Alternatif)

Nah, jika cara diatas terlalu panjang, berikut saya berikan rumus singkatnya:

Sehingga rumus x menjadi:

jadi jarak AB adalah 5000 m.

 

4. 

Sebuah mobil bergerak dari A ke B harus tiba di C. Jarak AB = 75 m, kecepatan awal mobil pada saat di A = 10 m/s dan percepatan antara A dan B adalah 2 m/s². Bila tinggi ujung B dari sebrang C = 5 m dan g = 10 m/s², maka hitunglah lebar lembah tersebut!

Pembahasan:

Diketahui:

voA = 10 m/s

sAB = 75 m

a = 2 m/s²

h = 5 m

g = 10 m/s²

Ditanya: lebar lembah ( misal x )

Jawab:

Dari A ke B mobil bergerak dipercepat, sehingga harus dicari terlebih dahulu kecepatan mobil saat dititik B (kecepatan sebelum melompati lembah)

VB² = v0A² + 2.a.s

VB² = 10² + 2(2)(75)

VB² = 100 + 300

VB² = 400

VB = 20 m/s

dengan cara yang sama seperti contoh 5, maka lebar lembah:

5. Jika sebuah selang air menyemprotkan air ke atas dengan kecepatan 10 m/s pada sudut 37^o berapakah jarak tempuh maksimum air tersebut.

Pembahasan

Dik : vo = 10 m/s; θ =  37^o.

xmax = (vo² sin 2θ)/g

⇒ xmax = (100 . 2 sin 37^o cos 37^o )/10

⇒ xmax = 20 (3/5) (4/5)

⇒ xmax = 9,6 m.

Jadi, air tersebut akan menyentuh tanah pada jarak 9,6 m dari selang.